1. How many different 8 letter words are possible using the letters of the word SYLLABUS?

• A. (8 – 1)!
• B. 8!/2!
• C. 8!/(2!2!)
• D. 8!

2. Evaluate: 16^0.16× 16^0.04 × 2^0.2

• A. 2
• B. 0
• C. 2⁰
• D. 1/2

3. Let ‘*’ and ‘^’ be two binary operations such that a * b = a22b and a ^ b = 2a + b. Find (-4 * 2) ^ (7 * -1).

• A. -49
• B. 64
• C. 113
• D. 15

4.

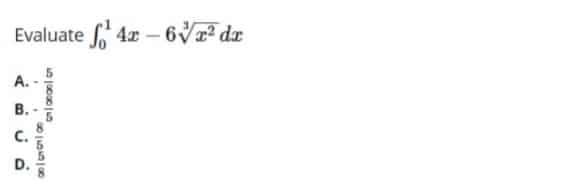
5. The population of a village decreased from 1,230 to 1,040 due to breakout of an epidemic. What is the percentage decrease in the population?

• A. 15.44%
• B. 15.43%
• C. 15.42%
• D. 15.45%

6. The interior angle of a regular polygon is five times the size of its exterior angle. Identify the polygon.

• A. dodecagon
• B. enneadecagon
• C. icosagon
• D. hendecagon

7. The area A of a circle is increasing at a constant rate of 1.5 cm²s⁻¹. Find, to 3 significant figures, the rate at which the radius r of the circle is increasing when the area of the circle is 2 cm².

• A. 0.200 cms⁻¹
• B. 0.798 cms⁻¹
• C. 0.300 cms⁻¹
• D. 0.299 cms⁻¹

8. Make x the subject of the formula: y = (3x−9c)/(4x+5d)

• A. x = −(9c−5dy)/(4y−3)
• B. x =( 9c+5dy)/(4y−3)
• C. x = (9c−5dy)/(4y−3)
• D. x = −(9c+5dy)/4y−3

9. Solve for x: 3(x – 1) ≤ 2 (x – 3)

• A. x ≤ -3
• B. x ≥ -3
• C. x ≤ 3
• D. x ≥ 3

10.

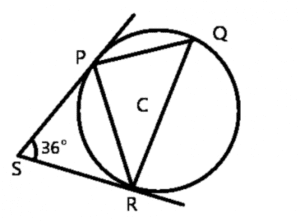
The diagram above is a circle with centre C. P, Q and S are points on the circumference. PS and SR are tangents to the circle. ∠PSR = 36^o. Find ∠PQR

• A. 72⁰
• B. 36⁰
• C. 144⁰
• D. 54⁰

11. If a car runs at a constant speed and takes 4.5 hrs to run a distance of 225 km, what time will it take to run 150 km?

• A. 2 hrs
• B. 4 hrs
• C. 3 hrs
• D. 1 hr

12. Divide 1101001_two by 101_two

• A. 11101_two
• B. 111_two
• C. 10111_two
• D. 10101_two

13. If (3−√3)/(2+√3) = a + b3, what are the values a and b?

• A. a = 9, b = -5
• B. a = 5, b = 9
• C. a = 9, b = 5
• D. a = -5, b = 9

14. Find the value of t, if the distance between the points P(–3, –14) and Q(t, –5) is 9 units.

• A. 3
• B. 2
• C. – 3
• D. – 2

15. At simple interest, a man made a deposit of some money in the bank. The amount in his bank account after 10 years is three times the money deposited. If the interest rate stays the same, after how many years will the amount be five times the money deposited?

• A. 15 years
• B. 25 years
• C. 20 years
• D. 30 years

16. Evaluate the following limit: lim_x→2 (x²+4x−12)/(x²−2x)

• A. 4
• B. 8
• C. 0
• D. 2

17. The ages of students in a small primary school were recorded in the table below.

Age	5 – 6	7 – 8	9 -10
Frequency	29	40	38

Estimate the mean

• A. 7.7
• B. 7.5
• C. 7.8
• D. 7.6

18. A committee of 5 people is to be chosen from a group of 6 men and 4 women. How many committees are possible if there is to be a majority of women?

• A. 60
• B. 15
• C. 66
• D. 4

19

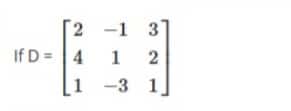
Find |D|

• A. 16
• B. 14
• C. -23
• D. -37

20. A boat sails 8 km north from P to Q and then sails 6 km west from Q to R. Calculate the bearing of R from P. Give your answer to the nearest degree.

• A. 217^o
• B. 323^o
• C. 037^o
• D. 053⁰

21. A coin is thrown 3 times. What is the probability that at least onehead is obtained?

• A. 7/8
• B. 3/8
• C. None the above
• D. 1/8

22. Find the equation of straight line passing through (2, 3) and perpendicular to the line 3x+2y+4=0

• A. 3y = 5x – 2
• B. y = (5/3) ×−2
• C. None of these
• D. 3y = 2x + 5

23.

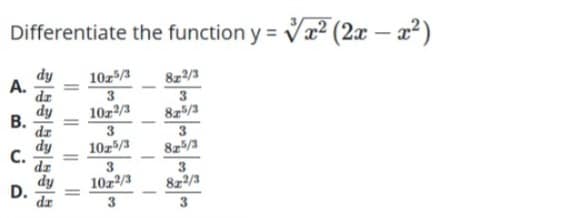
24. Calculate the mean deviation of the first five prime numbers.

• A. 2.72
• B. 5.6
• C. 5.25
• D. 13.6

25. Determine the area of the region bounded by y = 2x²+ 10 and Y = 4x+16.

• A. 18
• B. −10/3
• C. 44/3
• D. 64/3

26. Find the value of y if 402_y=102_ten

• A. 4
• B. 2
• C. 5
• D. 3

27. Find the value of y, if log (y + 8) + log (y – 8) = 2log 3 + 2log 5

• A. y = ±5
• B. y = ±10
• C. y = ±17
• D. y = ±13

28. In a group of 500 people, 350 people can speak English, and 400 people can speak French. Find how many people can speak both languages.

• A. 750
• B. 850
• C. 250
• D. 150

29. Factorize: 16x⁴−y⁴

• A. (2x−y)(2x+y)(4x²+y²)
• B. (2x+y)(2x+y)(4x²+y²)
• C. (2x−y)(2x−y)(4x²+y²)
• D. (2x−y)(2x+y)(4x²−y²)

30. If A = { 1, 2, 3, 4, 5, 6}, B = { 2, 4, 6, 8 }. Find (A – B) ⋃ (B – A).

• A. {1, 3, 5, 8}
• B. {8}
• C. {1, 2, 3, 4, 5, 6, 8}
• D. {1, 3, 5}

31. A bag contains 8 red balls and some white balls. If the probability of drawing a white ball is half of the probability of drawing a red ball then find the probability of drawing a red ball and a white ball if the balls are drawn without replacement.

• A. 1/3
• B. 2/9
• C. 2/3
• D. 8/33

32. The ages of students in a small primary school were recorded in the table below.

Age	5-6	7-8	9-10
Frequency	29	40	38

Estimate the median.

• A. 7.725
• B. 6.225
• C. 7.5
• D. 6.5

33. Find the matrix A

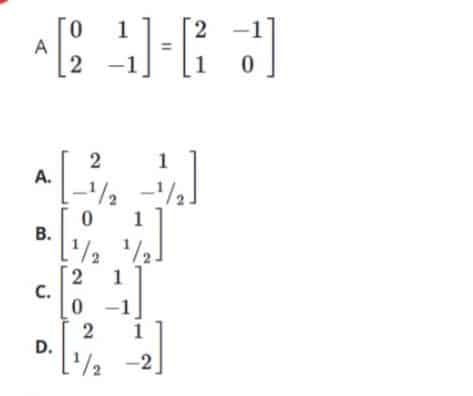
34.

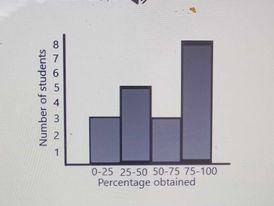
How many students scored at least 25%

• A. 16
• B. 19
• C. 3
• D. 8

35. If −2x³+6x²+17x- 21 is divided by (x+1), then the remainder is

• A. 32
• B. 30
• C. -30
• D. -32

36. Let a binary operation ‘*’ be defined on a set A. The operation will be commutative if

• A. a*b = b*a
• B. (a*b)*c = a*(b*c)
• C. (b ο c)*a = (b*a) ο (c*a)
• D. None of the above

37. Solve the following quadratic inequality: x²−x – 4 ≤ 2

• A. −3 < x < 2
• B. −2≤x≤3
• C. x ≤ −2 ,x≤3
• D. −2 < x < 3

38. What is the general term of the sequence 3, 8, 13, 18, …?

• A. 5n – 2
• B. 5n + 2
• C. 5
• D. 5n

39. The locus of a point equidistant from two intersecting lines is

• A. where the sum of the distances of two focal points is fixed
• B. the collection of points that are equally distant from a fixed point and a line
• C. the perpendicular bisector of the lines
• D. pair of bisectors of the angles between the two lines

40. Two numbers are respectively 35% and 80% more than a third number. The ratio of the two numbers is

• A. 7 : 16
• B. 3 : 4
• C. 16 : 7
• D. 4 : 3

41. The angle of elevation and depression of the top and bottom of another building, measured from the top of a 24 m tall building, is 30° and 60°, respectively. Determine the second building’s height.

• A. 24 m
• B. 32√3 m
• C. 24√3
• D. 32 m

42.

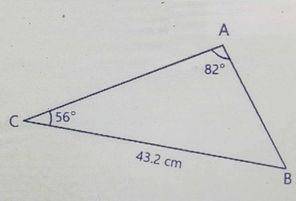
Calculate, correct to three significant figures, the length AB in the diagram above.

• A. 36.4 cm
• B. 36.1 cm
• C. 36.2 cm
• D. 36.3 cm

43. An article when sold for ₦230.00 makes a 15% profit. Find the profit or loss % if it was sold for ₦180.00

• A. 10% gain
• B. 10% loss
• C. 12% loss
• D. 12% gain

44.

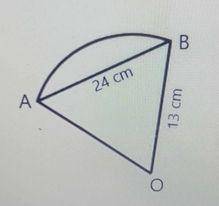
Calculate, correct to three significant figures, the length of the arc AB in the diagram above.
[Take π=22/7π=22/7]

• A. 32.4 cm
• B. 30.6 cm
• C. 28.8 cm
• D. 30.5 cm

45. A rectangular plot of land has sides with lengths of 38 m and 52 m corrected to the nearest m. Find the range of the possible values of the area of the rectangle

• A. 1931.25 m² ≤ A < 2021.25 m²
• B. 1950 m² ≤ A < 2002 m²
• C. 1957 m² ≤ A < 1995 m²
• D. 1931.25 m² ≥ A > 2021.25 m²

46. A man sells different brands of an items. 1/9 of the items he has in his shop are from Brand A, 5/8 of the remainder are from Brand B and the rest are from Brand C. If the total number of Brand C items in the man’s shop is 81, how many more Brand B items than Brand C does the shop has?

• A. 243
• B. 108
• C. 54
• D. 135

47. Find the area, to the nearest cm², of the triangle whose sides are in the ratio 2 : 3 : 4 and whose perimeter is 180 cm.

• A. 1162 cm²
• B. 1163 cm²
• C. 1160 cm²
• D. 1161 cm²

48. Find the compound interest (CI) on ₦15,700 for 2 years at 8% per annum compounded annually.

• A. ₦6,212.48
• B. ₦2,834.48
• C. ₦18,312.48
• D. ₦2,612.48

49.

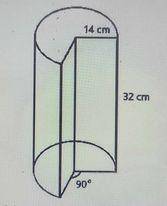
Find the volume of the cylinder above
[Take π=22/7]

• A. 9,856 cm³
• B. 14,784 cm³
• C. 4,928 cm³
• D. 19,712 cm³

50. The third term of an A.P is 6 and the fifth term is 12. Find the sum of its first twelve terms

• A. 201
• B. 144
• C. 198
• D. 72